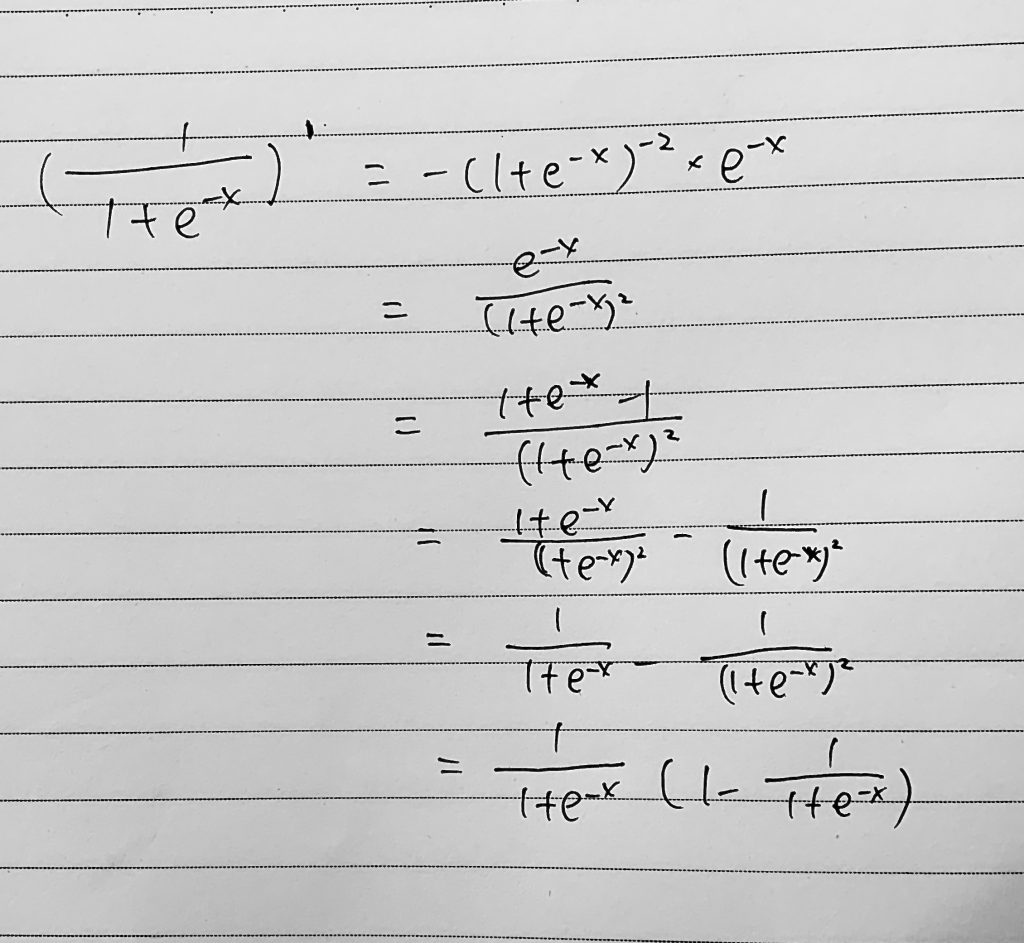源代码
先定义一些数据,X和y
1
2
3
4
5
6
7
8
| X = np.array([[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]])
y = np.array([[0],
[1],
[1],
[0]])
|
然后是sigmoid激活函数,deriv true是前向传播,就是常见的sigmoid,deriv false为反向传播,就是sigmoid求导的结果,如果不明白为什么是x*(1-x),可以看如下的求导,这里的x是sigmoid(x)
1
2
3
4
| def sigmoid(x, deriv=False):
if deriv == True:
return x * (1 - x)
return 1 / (1 + np.exp(-x))
|
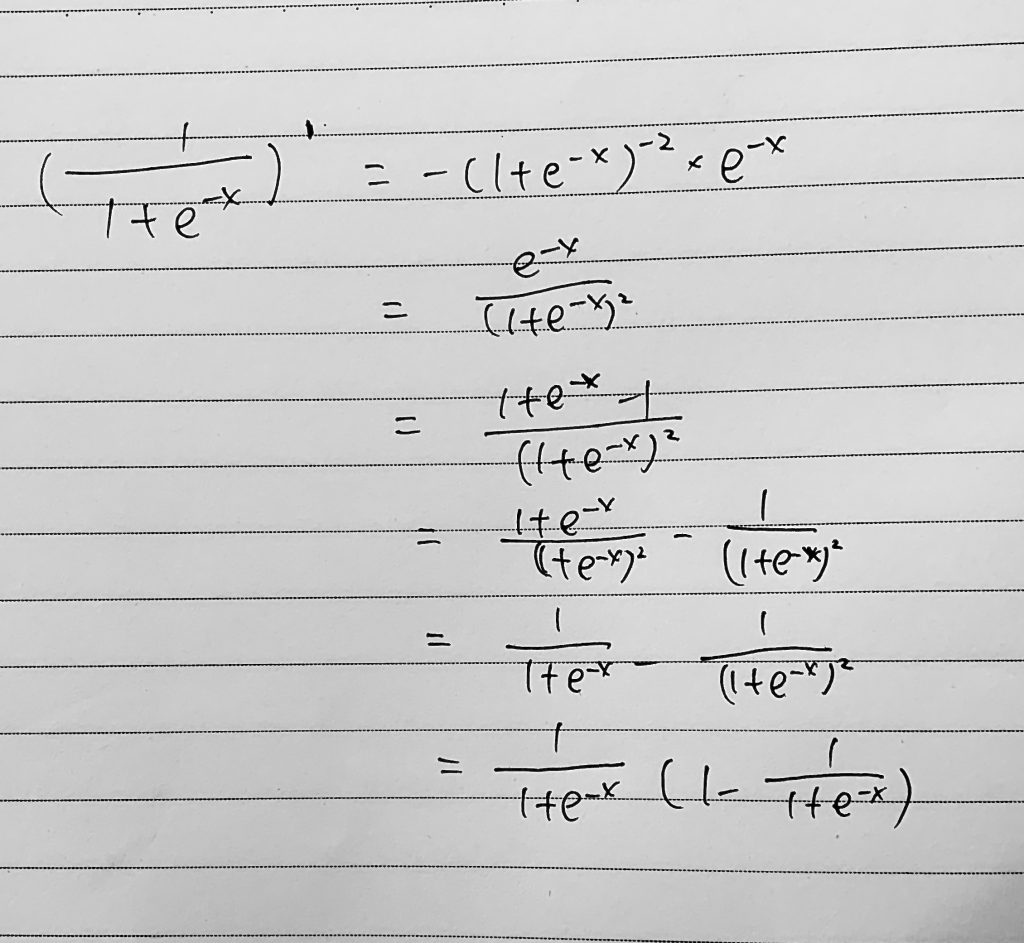
做一个两层的nn,这里的w0和w1映射到(-1,1),所以做了2和+1操作,注意维度,w0是和X相乘,w1是和(w0X)结果相乘。
1
2
| w0 = 2 * np.random.random((3, 4)) - 1
w1 = 2 * np.random.random((4, 1)) - 1
|
然后我们迭代一下,这里的l1和l2是正向,需要sigmoid。然后loss就是y – l2
l2_delta是反向,这里求导,l1_error和最后的loss是同理的,这两个sigmoid传入都是false。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| for j in range(50000):
l0 = X
l1 = sigmoid(np.dot(l0, w0))
l2 = sigmoid(np.dot(l1, w1))
l2_error = y - l2
if (j % 100) == 0:
print("err = " + str(np.mean(np.abs(l2_error))))
l2_delta = l2_error * sigmoid(l2, True)
l1_error = l2_delta.dot(w1.T)
l1_delta = l1_error * sigmoid(l1, True)
w1 += l1.T.dot(l2_delta)
w0 += l0.T.dot(l1_delta)
|